Problem : Most schools never clarify the essence of notation systems and the difference between a notation and its intended representation early on and expect people to just catch up later. To make a point its like drawing a round circle with two dots and an arc and calling it a ‘face’, thus confusing every such drawing as the very definition of ‘face’. Things will get clear as you read this post till the end, if things are still unclear, especially to new Renoisers.
Motivation: The simplest way to think of hex notation first is the number of increased symbols to represent more quantity or number of items. Babylonians used a base 60 system so you might imagine it’s a lot easier for us. The base of a number representation system really is a count of the total number of items that can be counted using a symbol from the symbol set. Once you get this part, you will suddenly see things very clearly and deal with ‘any’ base number like base 3 or base 7 or base 93 without any conceptual problems.
Instruction: Let us take a smaller number system like Base 3. The symbols in the symbol set can actually be any graphic or glyph that we like. However by tradition and convention we can certainly reuse existing symbols for familiarity and develop the symbol set. Base 3 = [0,1,2]. While we have 3 symbols, zero does not really denote a quantity but more a lack of or a starting point so in reality this symbol set will only represent 2 items. Why is it this way? Well that is why people tout the invention of zero as something more useful that just a symbol for an item, it effectively represents and empty placeholder or in real life and empty glass/tumbler and the number of items it will hold by virtue of its capacity. Interesting, is not it? This idea was invented or discovered by various cultures in the past but India was the first to ‘graphically’ symbolise or encode it, this giving birth to an entirely new (then) system of compactly representing numbers.
Now the first question one might ask is why is the last symbol ‘less’ by one from the base? To answer that, we have to remember that the symbols by themselves do NOT represent the total number of anything unless we attach some significance to it. Rather we take the total ‘number’ of symbols and use them like a mapping system for the total number of items that can be represented for each individual symbol greater than 0. The total count of symbols greater than 0 is 2, for our base 3 ‘notation’ system. You could make a symbol set like [tumbler,uno,duos] and that would work just as well. Now mapping things from the conceptual world to the circuit and electronics world required some amount of translation agreement or compromise and since switches that go on and off are essentially the next simplest form of encoding that can be done without hardware implementation issues, binary encoding system was developed. You can most definitely make a base 3 or base 9 computer but base 2 makes engineering design simpler and manageable.
Conceptual Visualization: The next step of understanding how to count in a similar base system is also easy and pure arthmetic. Basically you abstract a base number as the length of a drinking cylindrical shape tumbler, which we use to drink water. Also, you subdivide the glass length into carrom pucks that can fit into it.
This very powerful visualisation techniques will mean that for a base 3 system you essentially have a tumbler length that can hold 2 carrom pucks only. Same idea for base 10 or base 16, you have tumbler lengths that hold that many carrom pucks, which is base number-1 excluding the zero symbol, which is a placeholder.
Next step is now basically just using more tumblers to accommodate more carrom pucks to represent or hold higher quantities. So at this point a base (and the 0 symbol) represents a tumbler and the base number-1 the number of carrom pucks that can fit into a tumbler.
What next? Say you have your Base 3 glass full with 2 carrom pucks and you want to hold 3 pucks which is the next highest item count from base 3 symbol set, where do you put this 3rd carrom puck? Simplest way is to add another tumbler to your existing tumbler rack and slip a 3rd carrom to this empty tumbler. For sake of convention and consistency, we will add a new tumbler towards the left once the previous tumbler is full. Now at this point you have ALL 3 carrom pucks in the tumblers, but there is a representation issue now. What is it?
Encoding Consistency : Well, here is the distinction made between implementing a holding system and representing one, or notating one. The above arrangement is not at all too different from using the ancient 4 line parallel strokes and slashing the group in between for the 5th line making it very unweildy for large quantities. So the most essential benefit of having this base system of things is that you do not have to take into account each and every line/item that is being counted.
How? Well let us just empty the first tumbler and denote the new tumbler with the 3rd puck as ‘representing’ item 3. Becos to maintain error free encoding of this implementation, the earlier full tumbler must be emptied out so that it will not look it jumped from 3 items to 5 items suddenly. Think about it, it is every intuitive. So now the representation of quantity 3 in base 3 will look like 10. Becos the new tumbler now has only 1 carrom puck and the previous one is now empty, the number is almost like a histogram count of every tumbler basically that has more significance becos of its individual tumbler positions.
That is because each new position represents a new tumbler and each tumbler can hold only so many items , essentially you are using the ’ position’ of the tumbler to represent batches of items being counted. Now is not that more efficient? So the notation 100 will be 9 items in base 3 where you do not have to notate or store all 9 items but rather just 2 empty tumblers and 1 tumbler with one puck. Compact and nice eh?
This is how things should have been taught in school to everyone so that these conceptual gaps do not exist. If you understand the above, trust me on this one, you already understand the most fundamental and supremely important concepts of the birth of our civilisation and of computer science, and you have a leverage of many CS students or professionals who still have this concept unclear to them and they will always speak in terms of ‘dividing the number by the base’, but if you ask why, they can’t answer!! Try to pry and you will see for yourself.
So back to hex, basically it is a symbol set that uses numerical glyphs like 1,2 and alphabets from our common language to 'represent’more items than what our decimal system does by default. So now we have a mapping issue and much like the example from the base 3 instance above the same process is done for base 16.
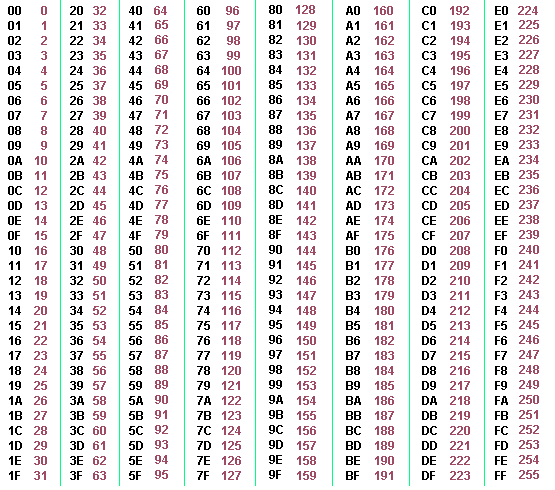
0xF represents the 15th item btw. Base 16 means 16 symbols for notation, one for each new item as it is accommodated while counting quantity. Once the 16th value is required to be counted you do the same thing. Place a new ‘tumbler’ to the left (paying ode to convention and consistency) and empty out the previous tumbler and place the 16th item in the new tumbler. This will effectively ‘represent’ the 16th item, this making the symbol now 0x10 for 16 items being counted for.
0x prefix is just a human language notation convention to denote base 16. Now you see, 10 in base 3 is 3 items; 10 in hex is 16 items and 10 in decimal is 10 items. See a pattern? The 10 symbol represents the base itself in every base notated this way.
Now why divide or multiply a particular notation symbol by its base to derive other bases. It’s basically math common sense. You just take a representation, and decide by the 'tumbler capacity’ to get the total number of items that is being counted, which makes sense does it not?
Say for 100 in base 3. By now we know that each new tumbler or position represents the base value in natural powers mostly because of the symmetrical manner in which the items are arranged conceptually. Each tumbler takes a fixed amount and each new position works as an ‘accumulator’.
So how we got to 9 items,let us check.
a) 1,2 for the first tumbler and the first two items. Then for the 3rd, we have 10.
B) 4th is 11. 5th is 12. 6th is 20. 7th is 21. 8th is 22 and 9th is 100. Get it?
So based on the patterns we see, we can derive a simple formula that works. 13^2+03^2+0*3^0 = 9 decimals in base 10.
Similarly for the base 16 numbers 0x11 is 17 decimals. The second 1 symbol on the left means that 16 items are already accounted for and the 1 in the previous or first position is a count of the 17th item. Again we can use the patterns that reveal from this techniques and just divide or multiply to map between bases.
The benefit is dance music is using 16 steps or beat subdivisions etc so 0x10 denotes 16 steps and 0x20 will be 32 steps and so on, which is why hex is so better for creative tasks when using computers. Also hex is the native language of all numeric representation in computer engineering above binary which makes you kill two birds with one stone. When you encounter the term “machine word size” it always is in multiples of 4, 8, 16, 32, 64 and so on.
Binary looks a lot more easy now does it not? b101 is what? We know from the above analysis and notation pattern that b10 is 2 in Base 2. So filling up each “tumbler” individually we arrive at 5 items 
BYTE data type : 0x0 to 0xF takes b0000 to b1111 and taking two such sequences or two hex characters/symbols we get an 8 bit binary pattern which is also known as a BYTE. Taking simple permutations of the binary symbol set to the length of the pattern : b1111 1111 we get 2^8 possible sequences which are unique. So now another popular representation that you get to see is in Prime number calculations where you will always see a number or a range denoted in the similar notation like 2^N-1. So now you know where this comes from and what it means. The minus one always gives the MAX value of the permutation range. Same for a 2^16 calculation for which the maximum value will be 2^16-1 or 65,535 MAX value from a possible value rangeof 65,536 values including 0; because this method of caluclation requires 0 to be included and therefore the maximum value is always minus one (for unsigned types). Thus 2^8-1 or 0xFF is 255 decimals.
Hope it helps