Can anyone recommend good books about keyboard / piano chord inversions?
So far the best looking book I can find is ‘progressive piano chords’ by Peter Gelling ( below ). Does anyone know of a better one?

Can anyone recommend good books about keyboard / piano chord inversions?
So far the best looking book I can find is ‘progressive piano chords’ by Peter Gelling ( below ). Does anyone know of a better one?

It really ain’t difficult .
When you have your normal triad / seventh chord …the basic rule is .
root + third +fifth + seventh = no inversion.
When the third is at root position = 1st inversion
fifth root = second inversion
seventh root =third inversion .
simple example , raising the fifth of a major chord by a whole step , gives you the first inversion of it’s relative minor
And when your lowering the root of a minor chord with a whole step , your playing the second inversion of it’s relative major …Etc
You really need a keyboard to have a feel of these inversions , cause they all depend on musle memory .
you could also play a C major with G-E-C in ascending order for instance… Not sure how one’d call this inversion.
Choosing an order for notes is more a matter of context (where’s the melody at this moment? do you want an ascending or descending movement, or none at all? What are the notes of the previous chord? You might want to maintain a “sensible” movement for each voice in a chord progression,each voice has a life of its own) and imagination.
Once you know how to build a chord (usually stacking up thirds, sometimes fourths…), I don’t think you really need a book about chords. Modes and scales might be a better insight to craft your chord progressions IMHO.
you could also play a C major with G-E-C in ascending order for instance… Not sure how one’d call this inversion.
Just a second inversion with open voicing .
That’s the word… “open”… Thanks 
I realize now I’ve always named open voicings by their notes only.
Thanks for the tips and inversions rules.
I was putting together a chords and harmonies composition guide.
I wanted to be thorough and scientific with it but all possible chords from a scale with all possible inversions will amount to hundreds per scale.
Knowing the rules of building inversions then just using them is better. I will leave inversions out of my guide thing.
the thing is , when you start to invert seventh chords , some chords will have the exact same keys …
It’s importan to identify the chord name within a given scale , reduces the overlap of naming , especcialy whe modulating outside of the scale .
Learn theory , the hardest part is to forgot what you have learned , serious !
the origin of the western harmony theory (and science) lies in astrolgy (12 notes 12 zodiac signs) or mnemonics (there were no books or were expensive) and not so much in listening habits
1 god
2 male / female
3 conditions - cardinal (out-going) fixed (expansive) mutable (returning)
4 elements - fire water air earth
7 planets = 3 conditions + 4 elements
12 zodiac = 3 conditions * 4 elements
12 is circular recurring
10 however (10 parts of the human body) is hierachically from top to bottom
1-10 from top to bottom and 1-12 around it is a three-dimensional sphere
In my experience, harmony is easiest to understand in conjunction with geometry
Here is a page with good examples
https://roelhollander.eu/en/blog-music/music-geometry/
another example with donald duck (6:50) pentatonic scale (is inside the 12 tones church scales) and a pentagram/pentagon
https://www.youtube.com/watch?v=U_ZHsk0-eF0
nice example (humans have pentatonic inside) with bobby mcferrin
lol
@ random:
Interesting article explaining how the 12 notes of the chromatic scale were originally made in ancient greece.
https://en.wikipedia.org/wiki/Pythagorean_tuning
Also, maybe you will enjoy these books:
And cymatics ( using vibration to create moving geometric patterns ) :
I think I have to step in here to bring some sanity to this thread…
The fundamentals of music is built upon universal harmonicity. It’s not something that was “made” or “invented” in Greece. It might have been discovered or systemized there, but the properties required to create our response to music are universal. The low integer ratios of overtones and scales aren’t coincidences, nor defined by the zodiak. 
The oldest known surviving written record of the structure of overtones and intervals ( dividing up a string ) is from Greece but the structure would have been pleasing to the ear and in use in any culture that enjoyed singing or flutes, didjeridoos, throat singing etc. (every human culture worldwide). Maybe even in non human cultures, birdsong, whalesong?
Tonic 1:1
The first overtone 2 : 1 ( octave ), the first interval - octave 2 : 1
The second overtone 3 : 1 ( fifth above the octave ), the second interval - fifth 3 : 2
The third overtone 4 : 1 ( two octaves ), the third interval - fourth 4 : 3
The fourth overtone 5 :1 ( two octaves and a major third ), the fourth interval - major third 5 :4
The fifth overtone 6 : 1 ( two octaves and a fifth ), the fifth interval - minor third 6 : 5
I think I have to step in here to bring some sanity to this thread…
The fundamentals of music is built upon universal harmonicity. It’s not something that was “made” or “invented” in Greece. It might have been discovered or systemized there, but the properties required to create our response to music are universal. The low integer ratios of overtones and scales aren’t coincidences, nor defined by the zodiak.
Thread saved from de-railing .
@Barrett Wang
interesting, looks similar to one of my favorite book
I think pythagoras interested especially in the physics of the sounds.
The pentatonic comes as far as I have noticed in all cultures in the world because it exists in nature within our perception (human voice, the sound of the wind)
The oldest known instrument in the world is a bones flute with these 5 notes
ptolemy extended the pentatonic with tetrachords (2 quadrilaterals) primarily as a convenience to take advantage of the number 12 “all-encompassing geometric scheme”
but that does not matter in today’s pop music
we mainly listen the last 100 years downgrade or back to the roots of 12 tone to blues to pentatonic to triad music 
Pentatonic scales are the nicest sounding to me, or the most peaceful sounding anyway.
All of the scales based around pentatonic. The japanese scales, the chinese scales.
Also the various overtone flutes sound beautiful.
here are some chinese and japanese scales:
Qing Shang : C Eb F G Bb
Qing Yu : C D E F G Bb
Quan Ming : C Eb F Ab Bb
Sakura : C Db F G Ab
Japanese? : C D Eb G Ab
Hirajoshi 1 : C E F# G B
Hirajoshi 2 : C Db F Gb Bb
Hirajoshi 3 : C D Eb G Ab
like the pentatonic too 
Here is a mnemotic with ptolemy tetrachords to the circle of quintets:
it is based on the dural ladder. the dural scale is subdivided into 2 so-called tetrachords each stem tone occurs 1 time in the scale.
2 tetrachords (or 2*4 Elements  ) are 7 tones because, for example, C is double (C-D-E-F and G-A-B-C)
) are 7 tones because, for example, C is double (C-D-E-F and G-A-B-C)
C D E F G A B
The structure of the tetrachords is identical: whole-tone-halftone
C D E F / G A B C
These two tetrachords are connected by a whole tone.
next you take the 2nd tetrachord of the scale and form the new durton leader on it GT GT BT (GT) GT GT BT
G A B C / D E F # G
D E F # G / A B C # D
A B C # D / E F # G # A
E F # G # A / B C # D # E
B C # D # E / F # G # A # B
F # G # A # B / C # D # E # F # (F # major consists of the same
Gb From Bb Cb / Db Eb F Gb Tones Like Gb Dur)
Db Eb F Gb / From Bb C Db
From Bb C Db / Eb F G Ab
Eb F G Ab / Bb C D Eb
Bb C D Eb / F G A Bb
F G A Bb / C D E F
C D E F / G A B C (there you are back at the beginning)
I think I have to step in here to bring some sanity to this thread…
The fundamentals of music is built upon universal harmonicity. It’s not something that was “made” or “invented” in Greece. It might have been discovered or systemized there, but the properties required to create our response to music are universal. The low integer ratios of overtones and scales aren’t coincidences, nor defined by the zodiak.
the map is not the territory, nothing is true, these are only tools
guitar - nice tool to play because you can transpose notes with the same fingering
keyboard - nice to see the difference between the pitches of the notes (halftone-whole-pitches or black white keys) but sadly not possible to play notes with the same fingering.
circle - in my option the best tool to understand musical theory because the old use the sky and the body to memorized and understandt these things
https://en.wikipedia.org/wiki/art_of_memory
and until today the wheel has not been complete reinvented every time
http://sound-colour-space.zhdk.ch/virtuallab/chromatic-scales
Try this website. Nice and clear explanations
http://www.piano-keyboard-guide.com/piano-chords.html
Also, maybe this layout is best. Like the thummer. Cant believe the thummer failed, looked awesome.

Thummer:
thummer looks nic, a little similar to chordion
http://www.olympianoiseco.com/apps/chordion/
keyboards need for me to much workspace, dont like it
try this for guitar
https://chordbook.com/guitar-chords/
back to off topic 
in the documentation notes and neurons (unfortunately only in french and german) https://www.youtube.com/watch?v=9JEPa4uAuv0
i heard for the first time that the harmonious and disharmonious perception of music is influenced by the culture
https://www.nature.com/articles/nature18635
In the past was no strict separation between music psychology religion and mathematic (since is young) likely more a hell of trying everything into a scheme
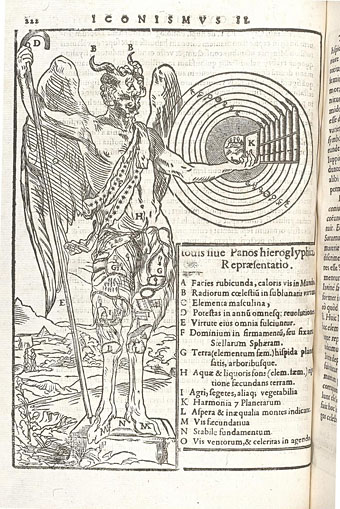
on the other hand, in the music literature it is said that the natural tone series can only be transposed to a limited extent without sounding disharmonic
that’s why we have well-tempered standart
https://en.wikipedia.org/wiki/The_Well-Tempered_Clavier
but why have a octave 12 tones, 7 white and 5 black keys?
easy to notice and sometime to understand with old school stuff 12 zodiac (circle) 7 old plantes (heptagram) and 5 parts of the body (pentagram)
random, universal harmony or cultural influence?
the origin of the western harmony theory (and science) lies in astrolgy (12 notes 12 zodiac signs) or mnemonics (there were no books or were expensive) and not so much in listening habits
1 god
2 male / female
3 conditions - cardinal (out-going) fixed (expansive) mutable (returning)
4 elements - fire water air earth7 planets = 3 conditions + 4 elements
12 zodiac = 3 conditions * 4 elements12 is circular recurring
10 however (10 parts of the human body) is hierachically from top to bottom
1-10 from top to bottom and 1-12 around it is a three-dimensional sphereIn my experience, harmony is easiest to understand in conjunction with geometry
Here is a page with good exampleshttps://roelhollander.eu/en/blog-music/music-geometry/
another example with donald duck (6:50) pentatonic scale (is inside the 12 tones church scales) and a pentagram/pentagon
https://www.youtube.com/watch?v=U_ZHsk0-eF0
nice example (humans have pentatonic inside) with bobby mcferrin
^This!
& this:
https://roelhollander.eu/en/blog-saxophone/Coltrane-Tone-Circle/