Lately I’ve been using pure data to make some single cycle waveforms .
For that I use an uzi object , which is bassically a recursive operation that fills a table object .
Connecting the cooefficients -variables to the trigger input of the uzi object ( which is blazingly fast ) we get a really fast gui update .
My question is , is lua capable of doing that , iow trigger a recursive operation exampel 2pi rad sin *sin pow^2 etc…and write that into an audio table (audio table = renoise sampler ) ?
This would explain the multiple audio tools for renoise , and I might consider learning the language .
1 Like
LUA, as any other OO-style (or better say functional) language, is capable of doing recursive calls and so traversing or creating recursive structures… If that is your question? You basically call the method within the method itself. There are various recursion patterns in informatics / computer science: Recursion (computer science) - Wikipedia
1 Like
I might be misunderstanding it but your example doesn’t seem like a necessarily recursive operation, more like a loop that executes an expression x number of times to fill a sample buffer (of course you can always implement loops as recursion as well).
In Lua, you can write both loops and recursive functions. The language even has proper tail calls to avoid stack overflow when running recursive operations.
Your function might look something like this (assuming you have an existing sample selected in an instrument)
local sample = renoise.song().selected_sample
local buffer = sample.sample_buffer
local length = buffer.number_of_frames
buffer:prepare_sample_data_changes()
-- loop over the entire sample
for i = 1, length do
-- convert position in sample to radians
local t = (i / length) * math.pi * 2
-- write a single frame into the sample
-- values are expected to be in the range of (-1..1)
buffer:set_sample_data(1, i, math.sin(t))
end
buffer:finalize_sample_data_changes()
This will write a single cycle of a sine wave over the entire sample. Of course in place of math.sin(t) you could have any other math expression.
In practice, you’d likely want to calculate stuff relative to the sample-rate instead of just the number of samples, but this is the gist of how to fill a sample buffer.
That being said, it might be better to use plugdata in Renoise if you want to change the parameters real-time.
For completeness sake, the same loop recursively would look like
function write_frame(buffer, i, length)
if i <= length then
buffer:set_sample_data(1, i, math.sin((i / length) * math.pi * 2))
-- the function calls itself recursively while incrementing i
return write_frame(buffer, i + 1, length)
end
end
local sample = renoise.song().selected_sample
-- call the function once to let it call itself until it runs out of frames
write_frame(sample.buffer, 1, sample.buffer.number_of_frames)Small brainfart , I meant iterative instead of recursive
Thanks for the explanation , makes it perfectly clear
This is possible on small chunks of audio.
There is only 1024 samples and this is a toy for lazy lua renoise scripting.
@gentleclockdivider, You can experience what you can do with the MUC (MIDI Universal Controller) tool, with the Waveform Sampler module, called “Wave Builder”. You can download the Demo version and try what it is capable of doing. You can use the mouse for this. You will see that iteration is a widely used resource!!!
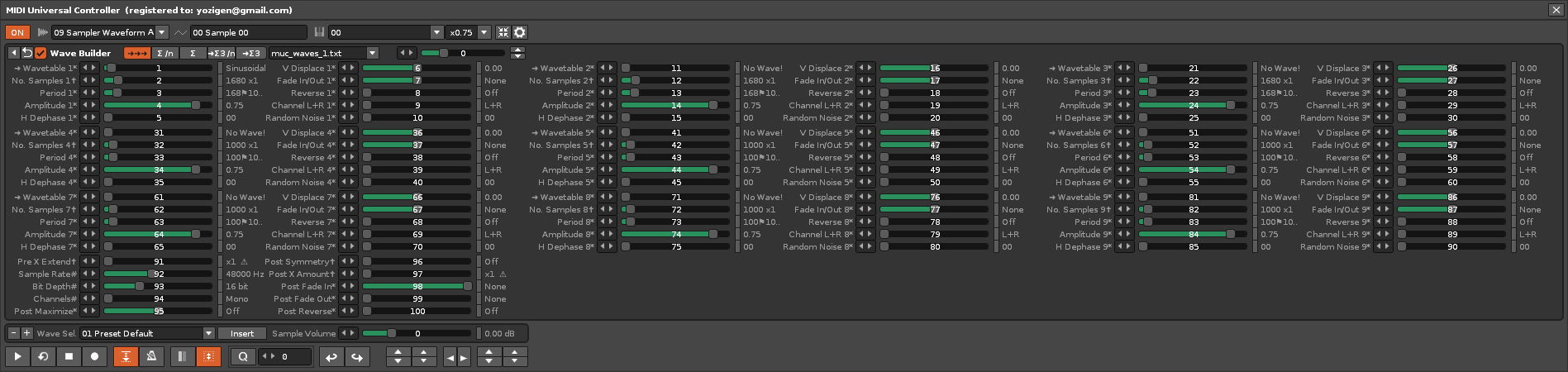
Basically, it is about creating points on an X-Y surface (frames-samples, amplitude) using mathematical formulas and destructively if you change the number of frames, simply combining the access provided by the API with the capabilities of Lua 5.1. This last condition of the change in the number of frames is slower or much slower as the table becomes larger. But, if you do not change the number of frames, it is not necessary to destroy the buffer to recreate it, so the result is very fast, even “in long audio waves”.
You can also work in mono (one channel) or stereo (two channels, twice as slow).
The problem with Renoise and its API is that to manipulate an audio wave of different duration (change in the number of frames) it is necessary to rebuild the buffer, that is, delete and create again, and if the buffer is large, the experience is becomes slow. So you have 3 scenarios with the same sample rate:
- Very fast. If the resulting audio wave lasts the same as the original. Here you don’t destroy the buffer, you just change the width of each frame. This is lightning fast.
- Fast: If the original and resulting audio wave are of short duration, 3-10 seconds, or something like that.
- Slow: if the original wave or the resulting wave has a very long and different duration. Rather the resulting wave, because it is necessary to destroy the original buffer and create a new long-lasting one.
In the MUC tool there are many examples of short and long waves. That’s why a small clock icon may appear in the process. It even allows you to save and tag your own created audio waves to reuse them later. It’s like a briefcase of audio waves with the ability to create/delete and reuse. I guess all this will give you an idea of what you can achieve. But the difficulty here is not the API or Lua, but the mathematical sciences.
In summary, if you work with audio waves with few frames (short duration), with a contained number of frames (see sample rate), you will have an instantaneous result in the user experience, it seems almost real time. And don’t forget that this is a CPU process. The faster the processor, the faster the user experience. Obvious.
Last added thoughts…
If you want to create an effective and fast tool, you can focus on always using a fixed number of frames, for example, with a specific sample rate that lasts about 5 or 10 seconds. This way you always use the same buffer (non-destructive) and you only need to change the amplitude of each frame. Then, you can create a silence at the end in each type of audio waveform (the last frames with amplitude=0).
That is, for example you can create waves of 1 second, 3 seconds or 10 seconds (all with 10 seconds):
- 1 second of wave, 9 seconds of silence.
- 3 seconds of wave, 7 seconds of silence.
- 10 seconds of wave, 0 seconds of silence.
This approach would practically allow changing the audio waveform “in real time” (instantaneous, with very few milliseconds of execution). You could even build a Lua tool that allows you to change the audio waveform on the fly linked to new pattern effects commands. No one has ever programmed that, but I’m sure it’s possible.
I’m not talking about whether such a tool would be useful or not. Perhaps it would even be absurd, since you can save an infinite number of audio waves before composing a pattern. But on an experimental basis it would be a lot of fun to create music with this approach, where even randomization according to certain parameters could create very fun sound things.
This thread should be here: https://forum.renoise.com/c/renoise-tool-development/
Wel I can already do it with pure data and reaktor , benefit of pure data is expressions on audio buffer ( expr~ ) where in reaktor it’s math modules . (be it in core or primary )
just wanted to know if lua is capable of doing it .
I got the answer
JFYI this also is available and pretty straightforward to use:
If you search in the forum, I posted some algorithms for it already, but none applying to your topic though.
Nevertheless it is a nice environment to quickly implement some real audio dsp using lua.