There are no steadfast rules but personally I always use Instrument Settings for anything sample based (IE tuning an individual sample) and Basenotes only for multisampled instrument assignment.
this makes sense to me.
cheatsheet tips&tricks section updated with my own Sorta Auto-Pan thingy (with xrns) and my own Alternative Native Delay trick > http://www.roaldblijleven.net/renoise/cheatsheet/tipstricks.php
The formula for frequency to midi note is: midi value= 69+ 12*log[sub]2/sub.
Fine tuning is 1/128 division of a semitone, so just multiply the decimal part of the midi value above by 128 to get the fine tuning required, which in this case will always be positive.
I wrote a script that does this calculation, which began because I had no idea how to find the frame length of a sample from inside Renoise. Anyway, it also converts to scientific pitch notation, saving any need to look up wikipedia, since I couldn’t find midi values in Renoise.
--calculation functions
function log2(x)
return math.log(x) / math.log(2)
end
function round(num)
if num >= 0 then return math.floor(num+.5)
else return math.ceil(num-.5) end
end
local samp_ind = renoise.song().selected_sample_index
local inst_ind = renoise.song().selected_instrument_index
local chosen_sample = renoise.song().instruments[inst_ind].samples[samp_ind]
local frames_selected = 1+(chosen_sample.sample_buffer.selection_end - chosen_sample.sample_buffer.selection_start)
--print(("Frames Selected: %s"):format(frames_selected))
local sample_rate = chosen_sample.sample_buffer.sample_rate
local freq = sample_rate/frame_total
--Converts to decimal MIDI value
local conversion = 69+(12*log2(freq / 440))
--print(("MIDI value: %s"):format(conversion)) --not needed
--Converts from MIDI to Letter name
function letter_name(x)
local midi_pitch = round(x)
local octave = math.floor((midi_pitch-12)/12)
local letter_table = { "C","C#","D","D#","E","F","F#","G","G#","A","A#","B" }
local letter = letter_table[(midi_pitch%12)+1]
print(("Note: %s%s"):format(letter,octave)) --prints A4 etc.
return letter
end
letter_name(conversion)
--Displays the fine tuning (negative or positive)
local finetuning = (round(conversion)-conversion)*128
print(("Finetuning: %s"):format(finetuning))
OK changed so that it calculates selected frames in the sample editor. If none are selected it calculates for all the frames.
@JupiterXLI: well, since i only half understand what you guys are talking about, i hope kazakore is very happy with your post! not sure if i should put this on the Cheat Sheet though, as only kazakore started about this, and now that he has the code he could just use that… or am i wrong? only thing i could do is place the code online or something as i don’t know what to do with it ![]()
Also, if I understood correctly, this could be a weapon of choice for tuning waveforms: Sample Loop Frequency Tool. It Seems it doesn’t support tuning to notes just yet, but the tool developer said this feature is already planned.
Wow thanks a load! Might take you code below and follow the basic instructions to try and make my first little tool ![]()
Note the highlighted section above. There are 255 finetune divisions in Renoise. I’m thinking maybe you should multiple by 255 and if the resulting number is above 127 then shift up by one note and use a negative finetune (255 minus sum result.)
No it’s only really useful to this specific context of tuning single cycle waveforms to higher precision in tuning samples or for converting between frequency, MIDI and scientific notation.
Doh! I made a mistake in the calculation it gives negative values which should be positive and vice versa, for example it says set the basenote higher and then fine tune down which will actually just get you back to square one. Anyway, the code does calculate negative and positive fine tuning, at least now it does, though I’m unsure of the benefit. Also I think that the 255 is divided into plus and minus 127, which makes tuning a lot easier, so I think there would still only be 128 between each semi tone.
ST1,1,2,3-------125,126,127,-127,-126,-125----------3,-2,-1,ST2 = 255 finetune divisions does it not?
OK I’ve done some tests and as far as I can tell your code works perfectly. Can’t pretend I understand 100% of the LUA but I am very happy, thank you so much ![]()
Something I have come across in my testing is that finetune goes from -1st 0st +1st over it’s range, not -0.5st 0st +0.5st as I had assumed. Not sure if that was the point you were trying to make but in any case it works!
How I know? I had examples of a tuned wave being in tune at A#2-65ft and this is 100% identical tuning to B2+63ft, which is the result given by your script.
Now I’m just going to look up a very minor modification, to change it from full sample to selected region, and then you can try it with more complex waveforms (at least tuning hit of drums and things like that.)
Also maybe change it to give transpose settings, as then it can more easily be used with layered instruments where you might have the same sample at different tunings…
currently having DNS problems. here’s a working link: http://roald.exul.nl/renoise/cheatsheet/
(1st post updated as well)
I just made a new wallpaper for referencing while composing inspired by your cheat sheet!

@Gooze: man that looks awesome! is it ok if i put it online on my cheatsheet so others can benefit as well?
Yeah, definately!
Here’s a PSD of a bigger version in case you want to make it fit your design:
http://www.mediafire.com/?6o15v1eop2ov2ci
I hope I haven’t made any mistakes on there… °___°
It’s the first time I’ve seen the ‘flat’ side with ‘sharp’ signs (in the circle of fifths). Hehe, From the top it’s C - F - Bb - Eb - Ab - Db - Gb. It’s a bit funny to call them ‘sharp’ scales and put ‘flat’ signs behind them isn’t it? ![]()
But you can’t make flats in renoise, only sharps T^T
Honestly though I always found music theory really obscurified and redundant. I know the historical reason for differencing between flats and sharps and I know that forquite a few instances it can be useful. But to me it really seems that 90% of musical theory is purely made for large orchestra playings. To most amateurs, bands and producers, it’s useless differencing something that is essentially the same. The same goes for natural minor scales, descening melodic minor scales all the other minor scales that are major scales with a different prime note.
I guess it shows that I am purely self taught.
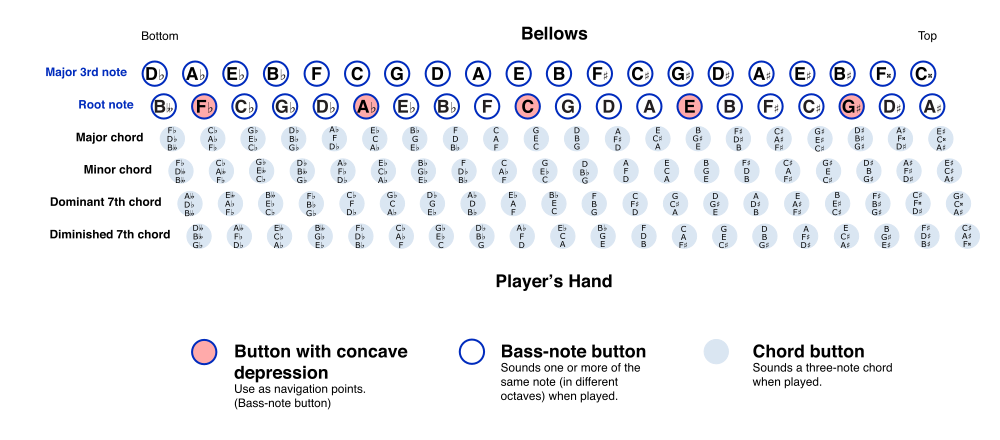
Btw. I never ever use the circle of fifths for other purposes than locating the bass buttons on my accordion, I always use the “circle of ones” for composing.
It’s about which notes are in the major scale.
So in Ab It’s Ab - Bb - C - Db - Eb - F - G
(A-B-C-D-E-F-G with a few flats)
If you would call that scale G#, you’d get a rather messy note followup in major scale: G# - A# - C - C# - D# - F - G
(G-A-C-C-D-F-G with a few sharps)
You see, you’ll get double G and double A notes. It’s fine if you can put everything together in your head but I don’t think you should put this out to anyone else since you’ll be presenting them very confusing information.
The beauty of the circles is that you can SEE how the system is build up, you’re changing it so it doesn’t make sense anymore, so why would you have it then ![]()
i’m eagerly awaiting the outcome of this debate before i make any changes to my cheat sheet ![]()
The only thing I’m trying to say is; you can put it in like this, but you obviously don’t understand what it stands for, so why bother then? If you’re not using it yourself, don’t confuse others that try to learn about the western scales. ![]()
Oh dear… I really hate Internet discussions. But here goes:
First of, I would agree that you (rhowaldt) probably should not put it on your cheatsheet for the reason that td6d stated: it is not the conventional way of representing it and therefore might be confusing to people who are learning. I fully agree on that point, and like I said I am self taught so I am the worst kind of authority on this point. Also you have a link to Suva’s chord machine which is better than my chart. However:
I love theory.
And saying that the circle of fifths is for telling the number of flats in a scale is really an understatement. It is like saying the the colour circle is for telling what the complimentary colour is. It is always the first usage of it that is mentioned but once you know the system, you won’t need the chart for doing it anymore.
What the circle of fifth is is a graphical chart showing the relationship of notes. It is arranged according to intervals of five half-tones because this gives even harmonic/consonant steps, as opposed to putting the up linearly as my “circle of ones” (I don’t know what it is actually called… circular chromatic graph?). The beuati of using such a circle for composing is that it is even, circular and doesn’t difference between octaves making it an ideal tool for transposing, figuring out a relative scale and finding your way out of a complicated progression.
And I do use it, just not for composing. If you’ve ever played the accordion you would know that the bass bellows is arranged accordingly intervals of fifths and since you are not likely to find an accordion arrangement for the song you want to play you often have make use with a piano arrangement. It comes in handy for translating.
I knew the intervals of the circle of fifths before I had even heard about it… I think it is a tool that all musicians can have joy of, not just pianists.
(I’m a terrible accordionist though)
The chart is the stuff I use when I compose and play music, I was just inspired rhowaldt to put it all up on one well organized page and I wanted to say thank you and show off that I know how to make dark glowy stuff in photoshop. I didn’t mean to do any harm… I always think in sharps because it helps me avoid getting confused, I can see how it would do the opposite for most musicians though. [details=“Click to view contents”] BUT NOT TRACKERS! TRACKERS DON’T USE ANY F*ING FLATS! A FLAT IS SOMETHING YOU LIVE IN! FLAME FLAME FLAME! SEND ME A TRACKER FILE WITH A FLAT IN IT AND I WILL CUT OF MY PINKY FINGER YAKUZA STYLE AND SEND IT TO YOU!
THERE IS NO F♭ THERE IS ONLY E♮! [/details]