New Tool (3.1) ChordGun

Raul · December 6, 2018, 5:22pm

Oh cool didn’t know about that Record & Play Filter, that does seem to solve the problem.

More inversion values were added to provide a greater range as a convenience, so you could easily fit a chord in a progression for smooth voice leading. For example it would be annoying if you went up two inversions and it’s still not high enough, so then you have to increment the octave and lower the inversions to make it fit. This allows you to keep going past the current octave, to fit it in without having to play with two levers

Ok, I’m using a virtual piano with 120 notes. So, to cover all the inversions, it is enough that you go to the next octave (there would be±2,±3 or±4 inversions in the chords of few notes, 3, 4, or 5 notes), since you can shoot each chord from any of the 120 piano notes (there are the 10 octaves directly).

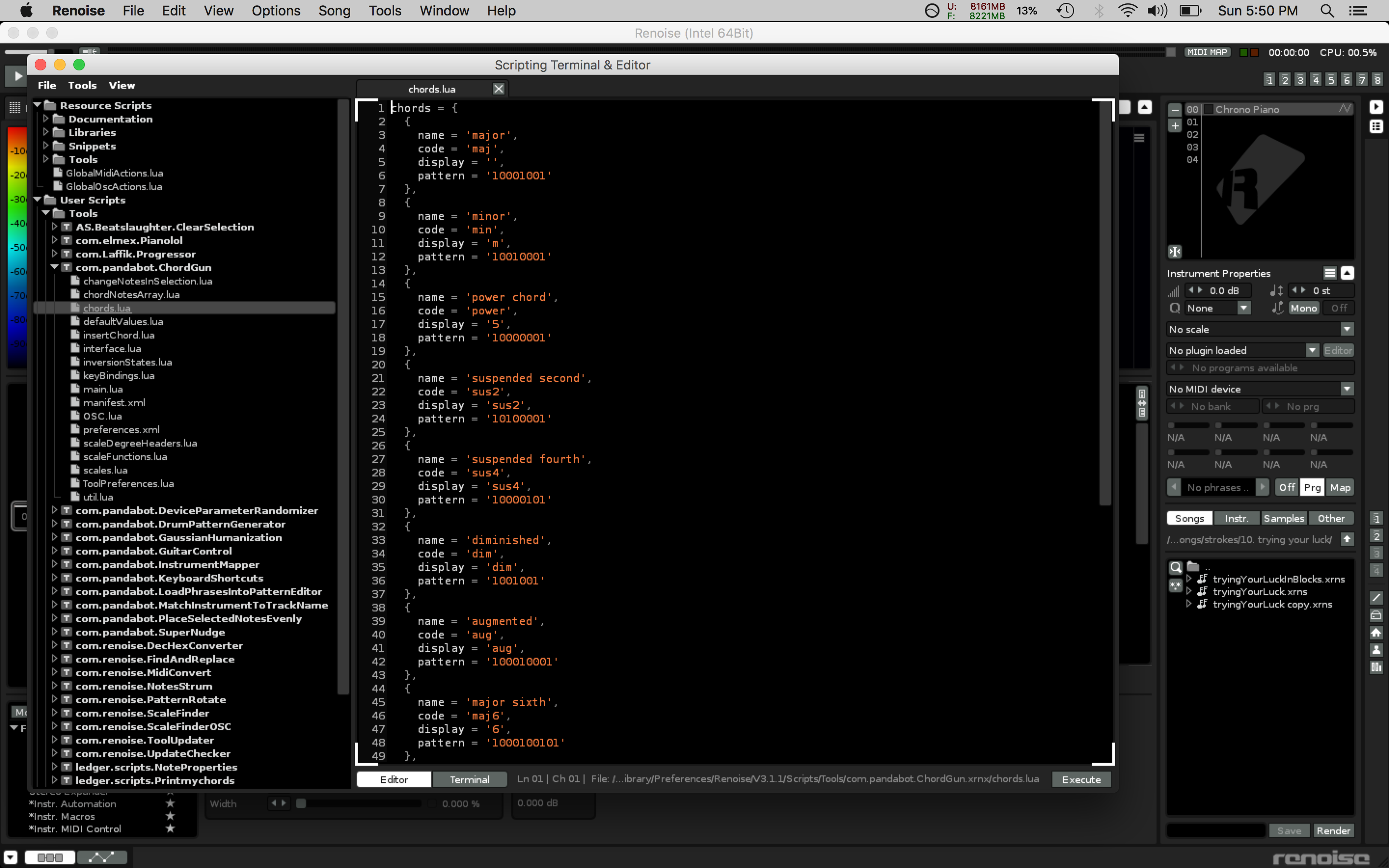
What I still have doubts is how to adjust each chord according to the scale. For example, I am using tables to define each chord, of this style:

For maj (no scale): {0,4,7}. How to convert this for all the scales that Renoise offers in the Instrument Editor (Natural Major, Natural Minor, 5 tone Scales…), in order to also add the inversions?

I’m using this table:

Click to view contents

PRE_CHD_VAL={ --24=121=empty
  {24,24,24,24,24,24,24},
  {0,4,24,24,24,24,24},
  {0,7,24,24,24,24,24},
  {0,4,7,9,24,24,24},
  {0,4,9,24,24,24,24},
  
  {0,4,9,14,24,24,24},
  {0,4,7,9,14,24,24},
  {0,5,7,9,24,24,24},
  {0,5,7,9,14,24,24},
  
  {0,4,7,10,24,24,24},
  {0,4,7,9,10,24,24},
  {0,4,7,10,14,24,24},
  {0,4,7,10,21,24,24},
  
  {0,5,7,10,24,24,24},
  {0,4,8,10,24,24,24},
  {0,4,7,10,15,24,24},
  {0,4,6,10,24,24,24},
  
  {0,4,7,10,13,24,24},
  {0,4,11,14,24,24,24},
  {0,4,7,9,10,14,24},
  {0,5,7,10,14,24,24},
  
  {0,4,8,10,14,24,24},
  {0,4,6,10,14,24,24},
  {0,4,7,10,14,17,24},
  {0,4,7,10,13,17,24},
  
  {0,4,7,10,14,17,21},
  {0,4,7,10,14,18,21},
  {0,4,7,10,13,17,21},
  {0,4,7,10,13,18,21},
  
  {0,4,6,10,13,17,21},
  {0,4,7,14,24,24,24},
  {0,4,8,24,24,24,24},
  {0,4,7,10,14,18,24},
  
  {0,4,6,24,24,24,24},
  {0,4,6,10,13,24,24},
  {0,4,8,10,13,24,24},
  {0,4,7,10,13,18,24},
  
  {0,3,6,24,24,24,24},
  {0,3,6,9,24,24,24},
  {0,4,7,24,24,24,24},
  {0,4,7,11,24,24,24},
  
  {0,5,7,11,24,24,24},
  {0,4,8,11,24,24,24},
  {0,4,7,11,14,24,24},
  {0,5,7,11,14,24,24},
  
  {0,4,7,11,14,17,24},
  {0,4,7,11,14,17,21},
  {0,3,7,24,24,24,24},
  {0,3,7,9,24,24,24},
  
  {0,3,7,9,14,24,24},
  {0,3,7,10,24,24,24},
  {0,3,6,10,24,24,24},
  {0,3,7,10,14,24,24},
  
  {0,3,7,14,24,24,24},
  {0,3,7,11,24,24,24},
  {0,3,7,11,14,24,24},
  {0,3,7,10,14,17,24},
  
  {0,3,7,10,14,17,21},
  {0,2,7,24,24,24,24},
  {0,5,7,24,24,24,24},
}

Do you also use tables or have you used any mathematical operation for each case?I’m dealing with almost 60 different chords between 3 and 7 notes.

pandabot · December 6, 2018, 6:46pm

I use a function that was written by either dread or suva, it seemed to work so I didn’t mess with it too much

function applyInversion(chord)
  
  local chordLength = #chord
  local chordInversionValue = getCurrentInversionValue()
  local chord_ = chord
  local oct = 0  
  
  if chordInversionValue < 0 then
    oct = math.floor(chordInversionValue / chordLength)
    chordInversionValue = chordInversionValue + (math.abs(oct) * chordLength)
  end
  
  for i = 1, chordInversionValue do
    local r = table.remove(chord_, 1)
    r = r + 12
    table.insert(chord_, #chord_ + 1, r )
  end
    
  for i = 1, #chord_ do
    chord_[i] = chord_[i] + (oct * 12)
  end

  return chord_
end

Raul · December 6, 2018, 7:01pm

I use a function that was written by either dread or suva, it seemed to work so I didn’t mess with it too much

function applyInversion(chord)
  
local chordLength = #chord
local chordInversionValue = getCurrentInversionValue()
local chord_ = chord
local oct = 0  
  
if chordInversionValue < 0 then
oct = math.floor(chordInversionValue / chordLength)
chordInversionValue = chordInversionValue + (math.abs(oct) * chordLength)
end
  
for i = 1, chordInversionValue do
local r = table.remove(chord_, 1)
r = r + 12
table.insert(chord_, #chord_ + 1, r )
end
    
for i = 1, #chord_ do
chord_[i] = chord_[i] + (oct * 12)
end

return chord_
end

Ah ok!I think I can create my own mathematical operation for my own tables, using a valuebox with -6 to +6 for the inversion of all my chords. It is only adding +12 or -12 to a specific value of the chord according to the inversion chosen.At least I can do it easily without using any scale.

Thanks!

Evert_Jonker_Trackah · April 10, 2019, 1:10am

Nice tool, i’m not so good with chords myself, and this makes things alot easier. thanks

Muad_39_Dib · June 20, 2019, 8:44pm

Awsome tool !! thanx.

EETTEE · June 30, 2019, 4:30am

Thanks for making this, this is easily the most useful tool I’ve come across! I’m not familiar with how OSC works, though. Does its use of OSC mean that it requires an internet connection to work?

rainydayshirts · June 30, 2019, 12:16pm

Just found this tool the other day. Simply fantastic. Excellent work.

helltrack · October 18, 2019, 6:42am

great tool, but what does the C1 trigger note option do?

pandabot · October 18, 2019, 5:50pm

If you use a guitar vst that needs an additional constant note to trigger a downstroke or upstroke

helltrack · December 1, 2019, 7:42pm

Would it maybe be possible to add little arrow keys inside ChordGun (maybe underneath the options), to move up and down in the pattern editor and quickly enter chords via clicking inside ChordGun?

Whenever I enter a chord the editor window loses focus and I have reclick on it to be able to move around again.

loving this tool <3

pandabot · December 1, 2019, 9:52pm

I’m not going to do that, but it is open source so that could be a good project if you’re interested enough. Otherwise I’d recommend using the keyboard shortcuts

helltrack · December 31, 2019, 12:48pm

I’ll start learning

trueschool · January 5, 2020, 4:11pm

I notice that ChordGun doesn’t seem to include 9th chords, something I use a lot on guitar. Is there a workaround or is there any plan to include those in future?
Thanks again for a supremely useful tool! I use it almost every time I Renoise.

pandabot · January 5, 2020, 10:55pm

I’m not going to do that but it’s pretty easy to add new ones, just go Tools->Scripting Terminal & Editor and open up chords.lua after expanding com.pandabot.ChordGun. You can see how they’re all defined in that file, you can add new entries in there.

jarzu3 · February 5, 2020, 1:16pm

has anyone added some extra chords themselfs by any chance? and if so willing to share the script.

trueschool · February 8, 2020, 7:32pm

I’d be willing to open up the chords.lua file and see if I can make sense of it as described above. Adding major 9th and minor 9th chords would be a good improvement that I think others would find useful. Is there a GitHub page for this plugin where I could contribute the changes back to the community, or is this the best way to share it back?

jarzu3 · February 8, 2020, 8:06pm

That would be really cool. I think people just post the code into the comments? im not sure tho never used it.

helltrack · March 27, 2020, 3:39pm

Actually I agree that adding Arrows in the GUI of ChordGun is unnecessary, but could you maybe allow pressing UP/DOWN still moving the Pattern Editor up and down, while ChordGun is focused?

I haven’t yet come around to learn LUA or Tool programming to do this myself, but I think it would be a nice general addition.

jarzu3 · November 17, 2020, 1:13pm

oh wow ! thanks for the work.

trueschool · November 17, 2020, 2:47pm

Yes, thank you so much! I get so much use out of this plug-in, I’d be happy to buy you a beer if you have a PayPal or Venmo or something. Thanks again!