Thanks to Nyquist and Shannon, analog to digital (and vice versa) conversions of audio samples has been thing since for awhile. And Renoise has this implemented into an instrument feature called interpolation (or resampling). Obviously you can read up from the wiki, but what I want to talk about is a certain application: resampling lo-fi audio samples and reproduce analog variants.
Let’s take a A-7 triangle wave generated from the Custom Wave Generator:
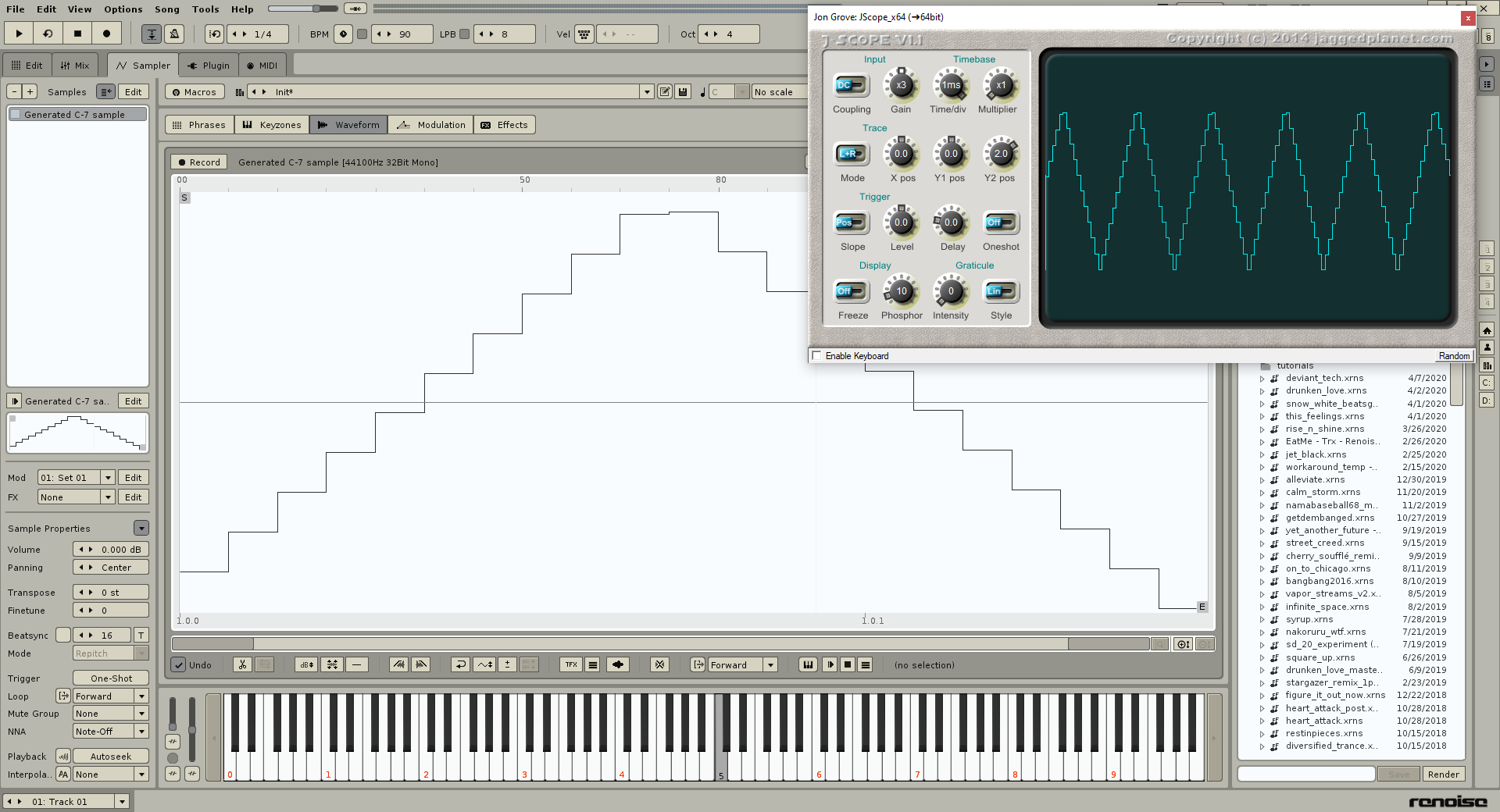
If you apply linear interpolation
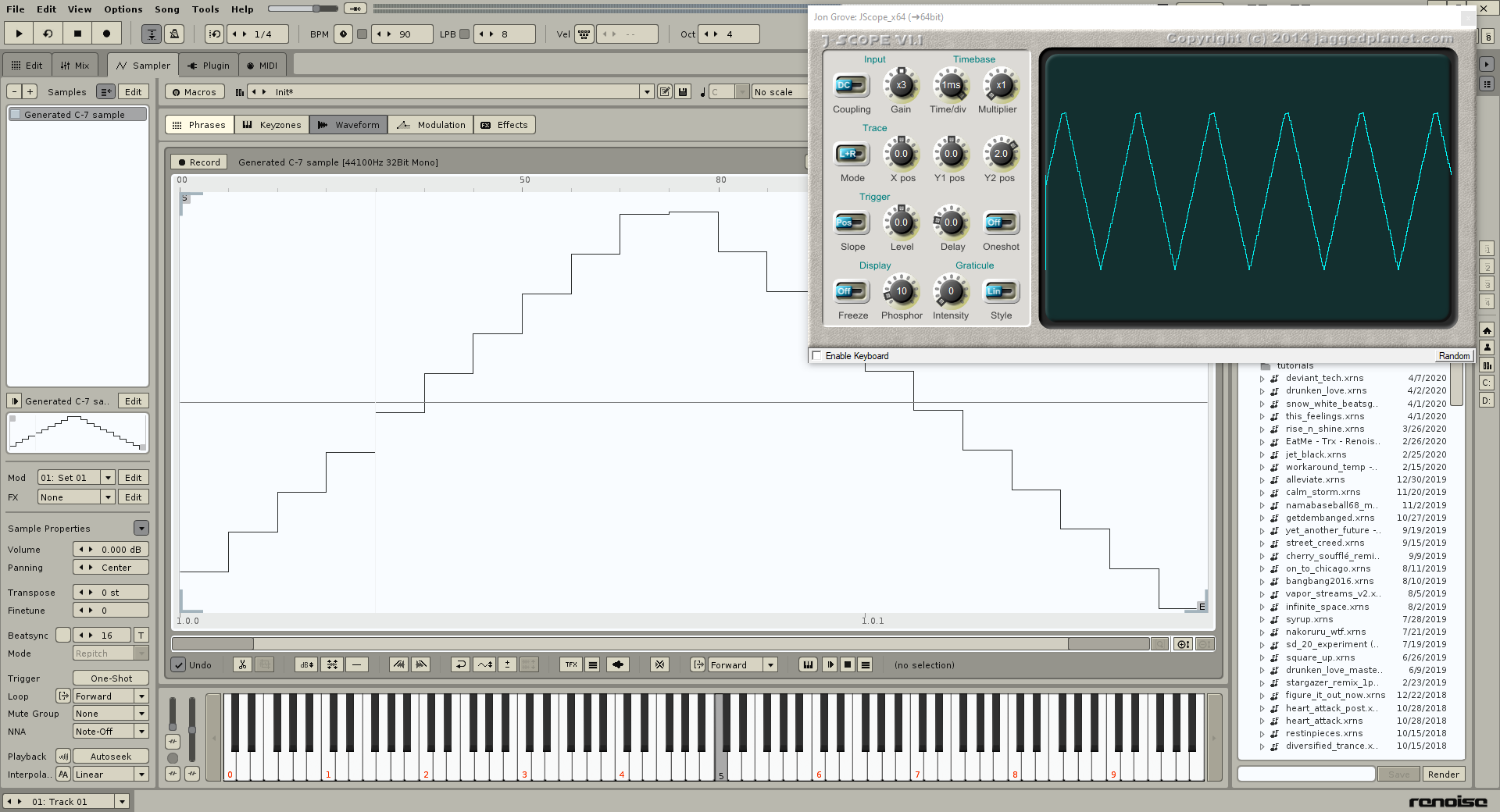
It’s very clear resampling the audio sample straightens out the waveform and produces a close to representation of a triangle wave. Sometimes due to the nature of the wave being resampled, the signal may not look pleasing at higher frequency.
So why is this important? Space saving! If you’re trying to save space in your project/computer this is great for this application. Now the only trade off is you need to use a little bit of CPU especially on low end PCs. These days CPUs are well made to the point I don’t think there’s not much tradeoff using Linear or Cubic Interpolation. Also depending on how the lofi sample is shaped, the interpolation can reshape it into not exactly what you expect, so experiment and look for different lofi-samples to your disposal!
Also… isn’t it preferable to have samples start at 0 DC?